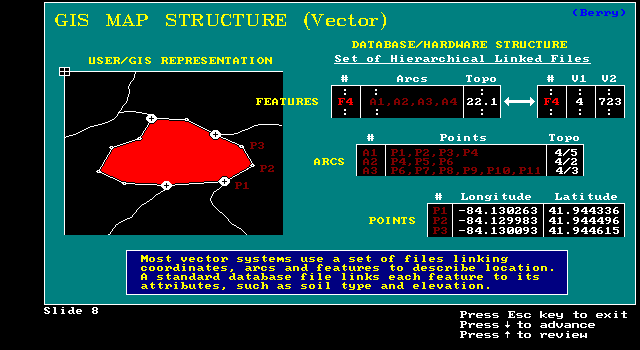
A cell on 1 map is at same position on all others
Easy query, neighborhood ops., etc.
concerned simply with what can be computed and what can't
contour for isoline model (variation on object model)
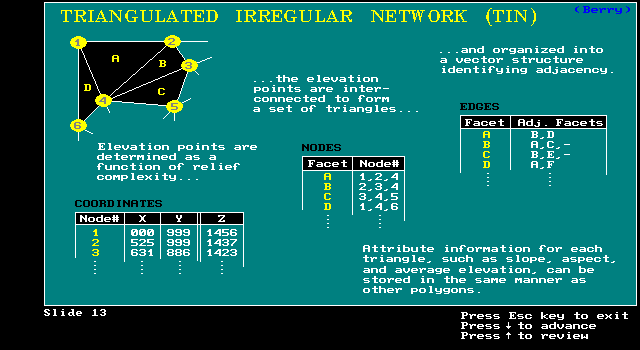
TIN for Delauney triangulation model
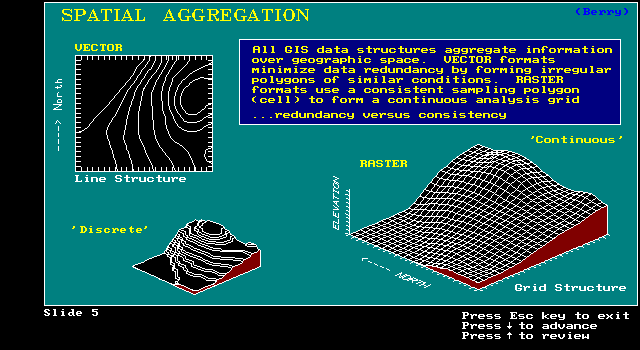
Raster is faster, but vector is corrector
uniqueness/irregularity of map features
data structuring must be more complex
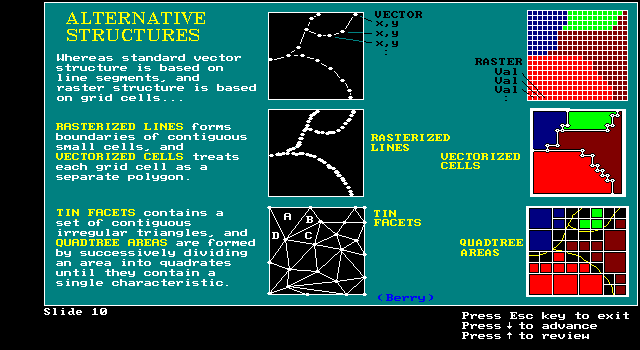
Increased processing speeds/storage allow for alternatives
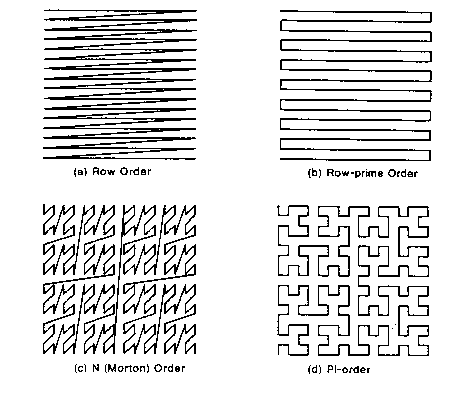
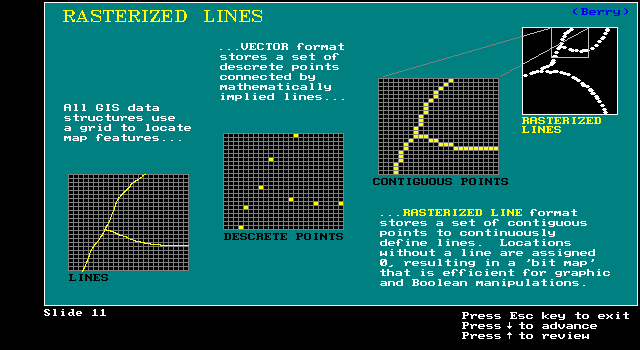
Rasterized Lines:
grid structure characterizes line
hardware loves this format
scanners, screens, plotters,fax machines
fast array/parallel processing
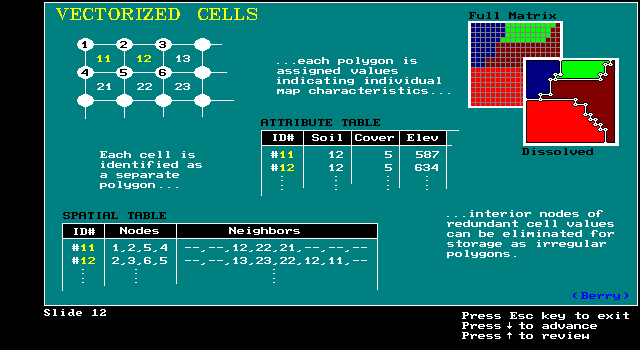
Vectorized Cells:
raster to vector conversion
connect centers of cells w/ similar value for lines
points are centers of cells
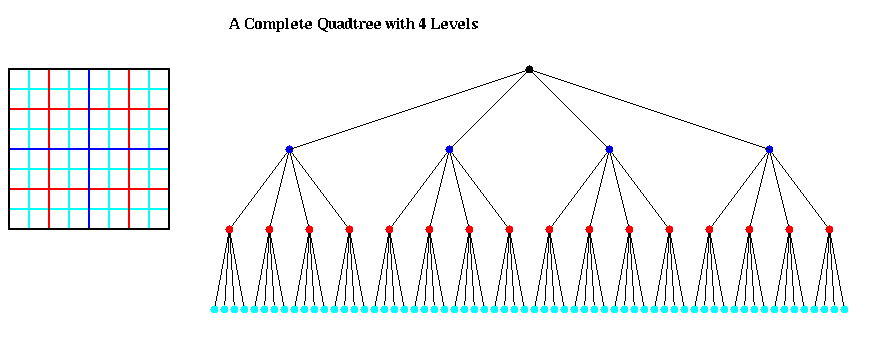
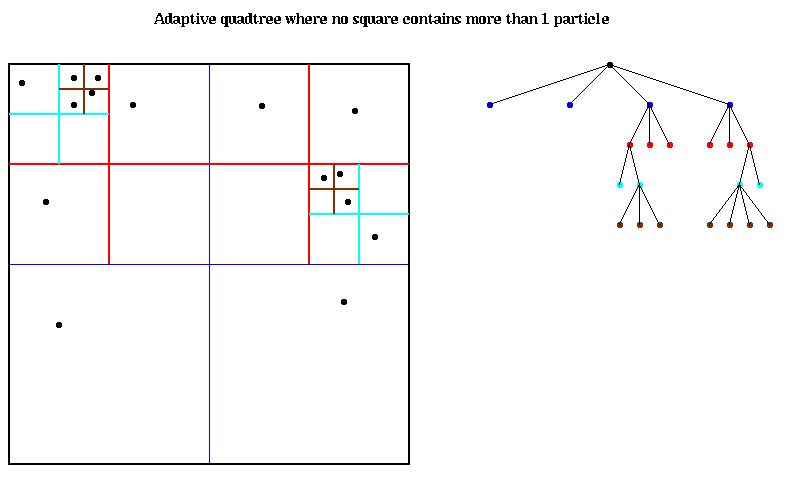
Divide into sub-quadrants
Focusing on irregularity
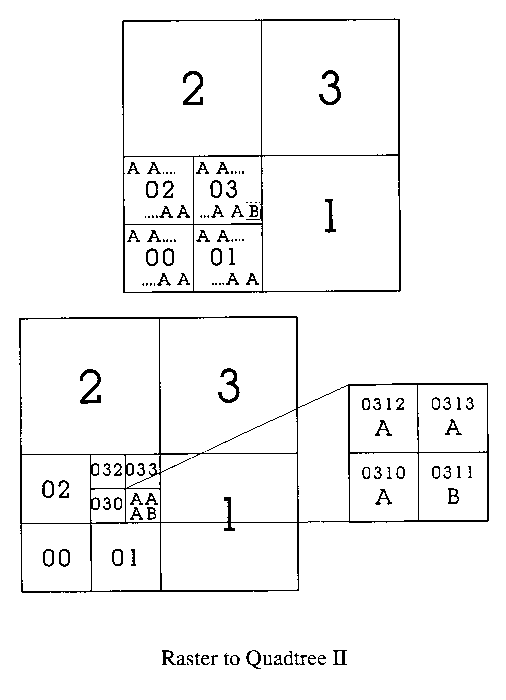
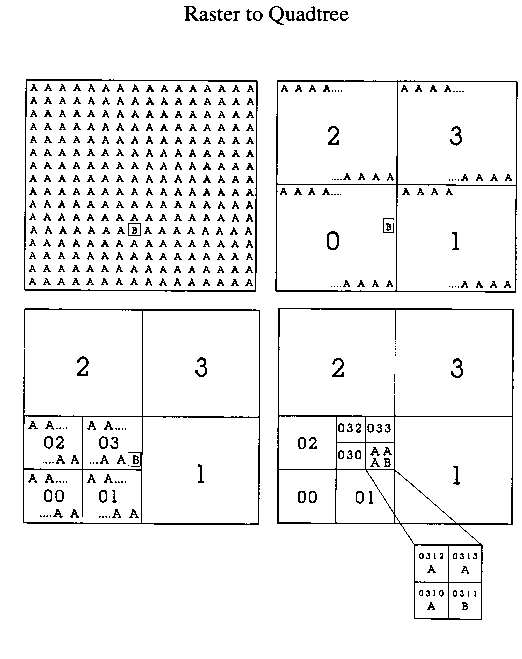

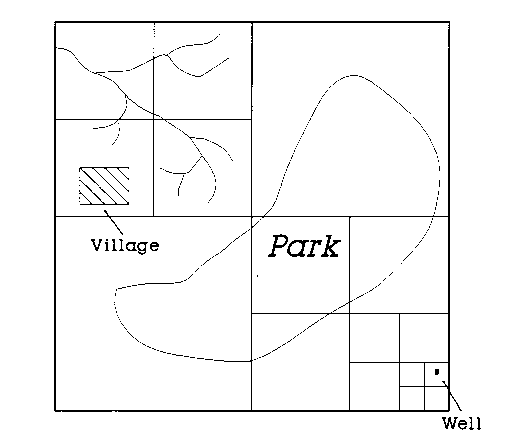
Code of well in map below is 1112
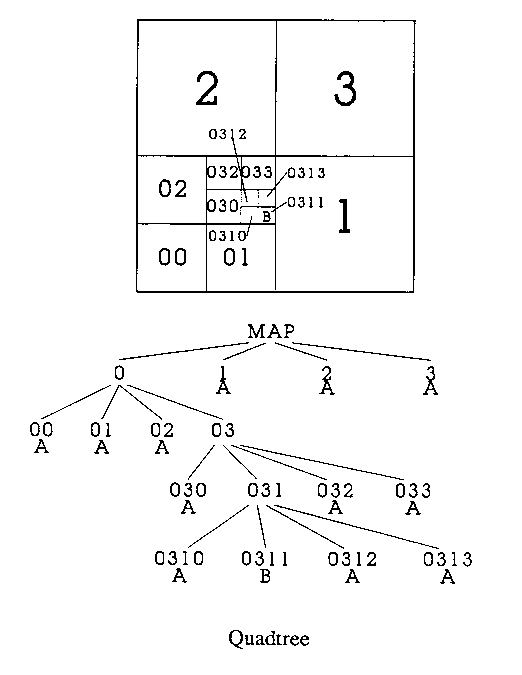
Another way to think of a quadtree is a means of encoding an image as a tree structure. Each node of the tree has up to four children. The root node represents the entire image; its children represent the four quadrants of the entire image; their children represent the sixteen subquadrants; the children of those represent the sixty-four sub-subquadrants, and so on.
more efficient than raster for some terrain analysis
-- slope and aspect (faces of triangles) measurements irregularly spaced with more sampling in areas of greater complexity
-- requires fewer points or grid cells